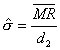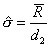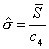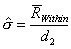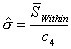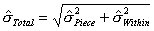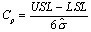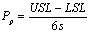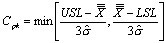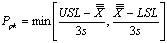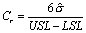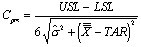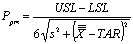盈飞无限在您身边
业务咨询:
marketing@infinityqs.cn
在线服务:
service@infinityqs.cn
电话:400-812-1268
010-65699909
业务咨询:
marketing@infinityqs.cn
在线服务:
service@infinityqs.cn
电话:400-812-1268
010-65699909
标准偏差和能力指数
|
||
短期波动性一般用“过程标准偏差”或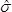 (见表1)来表示。 长期波动性表示为“样本标准偏差”或s (间见公式1)。尽管这两个标准偏差都是用来描述波动性的,但它们的计算和解释都有很大的差异。 (见表1)来表示。 长期波动性表示为“样本标准偏差”或s (间见公式1)。尽管这两个标准偏差都是用来描述波动性的,但它们的计算和解释都有很大的差异。 |
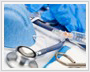
短期标准偏差 (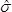 ) ) |
||||||||||||||||||||||||
|
如果控制图的极差、移动极差或 s 图是受控的,那么则表示子组和子组波动性是稳定和不变的。极差、移动极差和 s 统计量都是子组内部波动的量度,短期内波动的量度。 在可见的控制图中,独立数据的标准偏差是从不同的图表中用表1的公式计算得出。表1的公式是用来计算短期标准偏差(σ) ,和过程能力指数 Cp、Cpk、 Cr 和 Cpm 的(见图2)。ProFicient 可以使用表1中的任何公式计算σ。 |
||||||||||||||||||||||||
|
||||||||||||||||||||||||
| 长期标准偏差(s) |
长期标准偏差 s (通常称之为“样本标准偏差”),是通过对单个数据和它们的总体平均值之间的差值求和计算(公式1)。其中的总平均值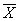 ,在公式中是用来当作长期波动的评估,这是长期偏差和短期偏差的关键区别。 ,在公式中是用来当作长期波动的评估,这是长期偏差和短期偏差的关键区别。 |
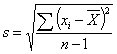 |
|
公式1 长期波动的评估s |
| 长期标准偏差s ,是用来计算过程性能指数的,包含Pp、 Ppk、Ppm和Pr。 |
| s 和 σ的区别是什么? | ||||||||||||||||||||||||||||||||||||||||||
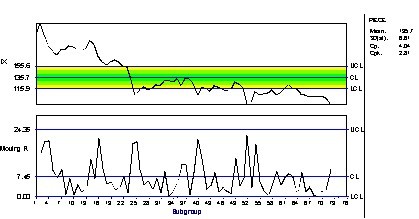
| 见图1.移动极差图可控状态,表明短期波动性没有出现变化。然而,单值图表现出了明显的下降趋势。这种下降趋势是长期总平均值下降的例子。也就是说,长时间内的波动发生了显著的变化。 | ||||||||||||||||||||||||||||||||||||||||||
 |
||||||||||||||||||||||||||||||||||||||||||
|
图1 IX-MR 图在长时间内的波动性 |
||||||||||||||||||||||||||||||||||||||||||
如果 IX 和 MR 表在一段时间内保持一致,短期和长期波动估计将接近一致。但是,如果平均值随着时间发生了显著的变化,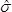 就不能包含这种波动性,因为 就不能包含这种波动性,因为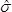 仅是短期波动性的评估,( 仅是短期波动性的评估,(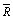 或者 或者 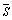 )。过程标准偏差, )。过程标准偏差,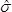 忽略 忽略 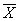 和任何值的变化。这是 和任何值的变化。这是 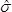 和 s 的主要区别。 和 s 的主要区别。能力指数也存在同样的问题,有时候人们会把Cp 和 Cpk 值混淆。注意,在图右边的 Cp 和 Cpk 值都大于1.33,这表明,尽管存在趋势,但所有的产品都在规格限内。然而,问题并不在于此。Pp 系数 (使用长期波动性估值s) 等于0.76 ,而Ppk=0.65。每个指数都远远小于相应的 Cp 和 Cpk 值,表明产品超过了规格限。因为长期波动性是变化的,所以 Pp 和 Ppk 比可以更准确地反映过程能力。 如果在能力指数中忽略了下面的波动性的计算,得到错误的报告,可能会导致做出错误的判断。 |
||||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||||
相关文章
【质量改善】一个与粉笔有关的质量管理故事…
领导拍板放行,质量人该如何应对?
【全面质量管理】带你无死角剖析全面质量管理
【SPC】让SPC来指引你走向质量管理信息化的道路
【质量管理】质量管理,你必须要做出的转变
【供应商】质量管理工作中的疏漏—供应商管理
客户案例