盈飞无限在您身边

业务咨询：
marketing@infinityqs.cn

在线服务：
service@infinityqs.cn

电话：400-812-1268
010-65699909

在一个控制图上监控多个过程

多个过程流

在很多行业中，通常需要控制多个独立的过程流，这些过程生产相同的产品。在此例子中，我们监控一个灌装机上的八个灌装头（这些灌装头是独立的，因为每个灌装头上有独立的灌装泵）。

在表格1中20个数据样本表示每个灌装头的灌装量。每 15 分钟进行一次取样。

图1：八个灌装头的注射机。每个灌装头由独立的灌装泵控制。

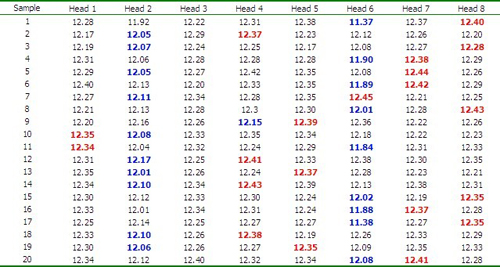
表1:数据表示 20个样本。每个样本中包含八个容器（每个灌装头一个），每隔15 分钟取样一次。红色的值为样本的最大值，蓝色的值为最小值。

组图分析

对于每个样本，最大值和最小值在单值（IX）图（图2，上）上显示。移动极差由每个样本中每个灌装头的值计算，将移动极差的最大和最小值绘制在移动极差图上（图2，下面的图）。比如，在样本2中，灌装头 4 的移动极差为最小，是|12.31- 12.37| = 0.06，灌装头6 的移动极差最大，是|11.37- 12.12| = 0.75。

中心线表示所有数据的平均值，不是最大值和最小值的平均值。控制限、短期西格玛和Cp/Cpk 是基于八个灌装头总体标准差计算的。

图 2: 组图 IX-MR 中，单值IX图显示了最大和最小值，移动极差MR显示了所有样本移动极差的最大和最小值。两个图中都包含了几个超出控制限的点。

在理解组图时，需要在图上找到最大和最小的位置。在单值图上，注意到最小值中灌装头2和6 很多。表明这些灌装头的灌装量总是小于其它灌装头。同时，移动极差中的最大值主要是灌装头6。表示此灌装头的波动比其它灌装头更大一些。

在箱线图上查看多个过程流

组图对查看一段时间内多过程的行为非常有用。另一个用于对比多个分布的工具是箱线图。像直方图一样，箱线图显示数据的分布（图3）。直方图是正视图，而箱线图是俯视图。

图 3: 箱线图说明

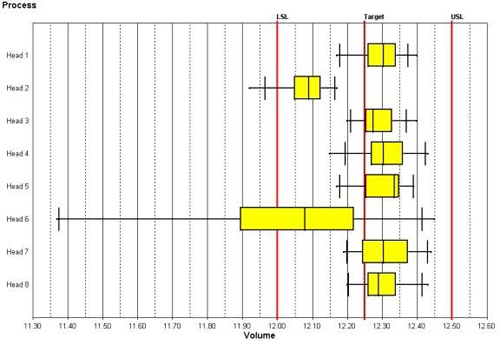
请注意，箱线图（图4）中清楚地显示了灌装头2和灌装头6的灌装量小于其它灌装头。同时，灌装头6 的波动也最大。这样的结果和组图所解释的结果是完全吻合的。

在用户的 SPC 程序中，使用组图和箱线图将显著的提高 SPC

图 4: 箱线图显示了每个灌装头的灌装量分布。注意，灌装头2和灌装头6的灌装量已经在公差限以下。