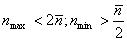SPC控制图的绘制与判断
关键词:SPC控制图,控制图,控制界限
主要内容:
绘制程序
各类控制图作法举例
控制图的观察与判断
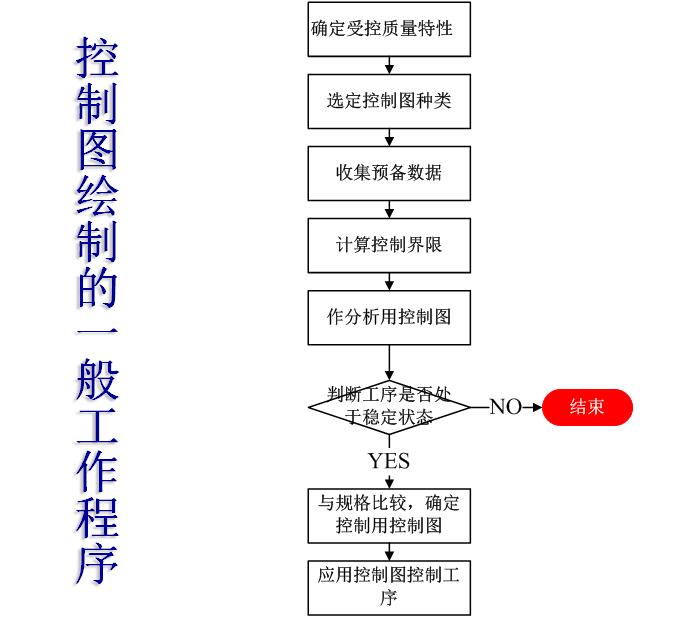
绘制程序:
1确定受控质量特性
即明确控制对象。一般应选择可以计量(或计数)、技术上可控、对产品质量影响大的关键部位、关键工序的关键质量特性进行控制。
2选定控制图种类
3收集预备数据
4计算控制界限
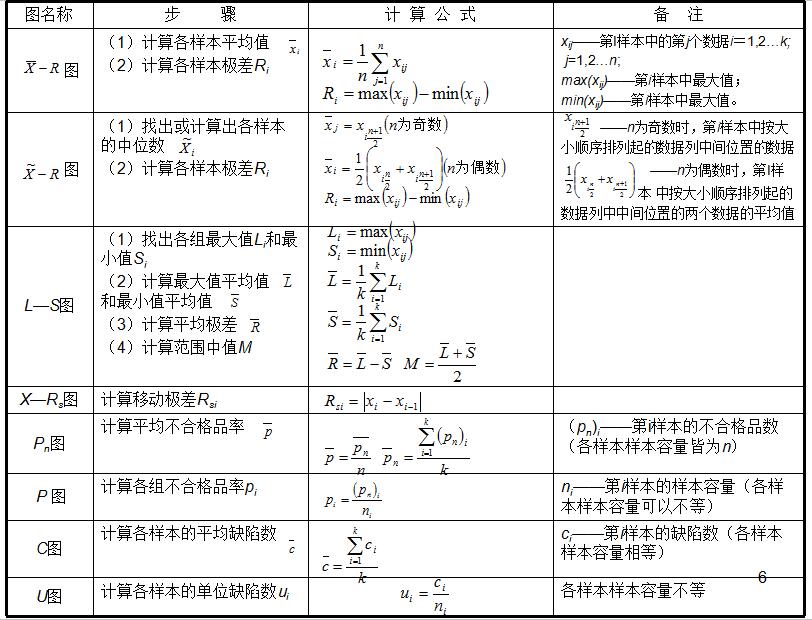
各种控制图控制界限的计算方法及计算公式不同,但其计算步骤一般为:
(1)计算各样本参数(见表3);
(2)计算分析用控制图控制线(见表4)。 5作分析用控制图并判断工序是否处于稳定状态
6与规格比较,确定控制用控制图
7应用控制图控制工序
控制用控制图制好后,即可用它控制工序,使生产过程保持在正常状态。
3 收集预备数据
收集预备数据的目的只为作分析用控制图以判断工序状态。数据采集的方法是间隔随机抽样。为能反映工序总体状况,数据应在10~15天内收集 ,并应详细地记录在事先准备好的调查表内。数据收集的个数参见表2。
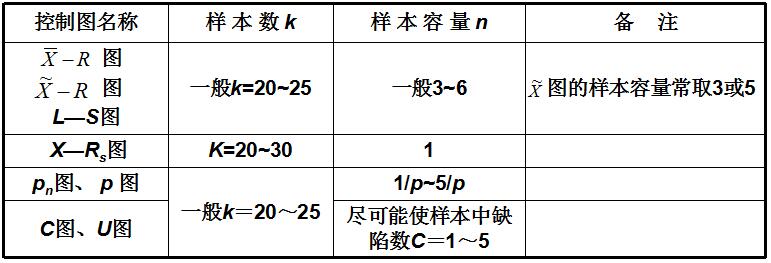
表2 控制图的样本与样本容量
4 作分析用控制图并判断工序是否处于稳定状态
在坐标图上画出三条控制线,控制中线一般以细实线表示,控制上下线以虚线表示。
将预备数据各样本的参数值在控制图中打点。
根据本节介绍的控制图的判断规则判断工序状态是否 稳定,若判断工序状态不稳定,应查明原因,消除不稳定因素,重新收集预备数据,直至得到稳定状态下分析用控制图;若判断工序处于稳定状态,继续以下程序。
5与规格比较,确定控制用控制图
由分析用控制图得知工序处于稳定状态后,还须与规格要求进行比较。若工序既满足稳定要求,又满足规格要求,则称工序进入正常状态。此时,可将分析用控制图的控制线作为控制用控制图的控制线;若不能满足规格要求,必须对工序进行调整,直至得到正常状态下的控制图。
所谓满足规格要求,并不是指上、下控制线必须在规格上、下限内侧,即UCL>TU;LCL< TL。而是要看受控工序的工序能力是否满足给定的Cp值要求。
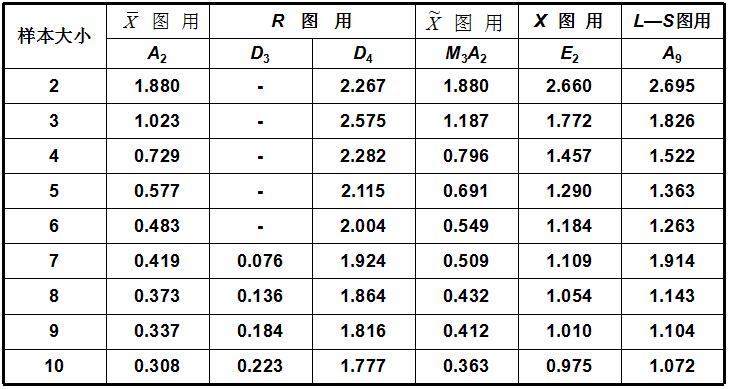
表5 控制图系数表
各类控制图作法举例
1.x-R控制图(平均值——极差控制图)
原理:
x图又称平均值控制图,它主要用于控制生产过程中产品质量特性的平均值;
R图又 称极差控制图,它主要用于控制产品质量特性的分散。
“x-R”控制图是通过 图x和R图的联合使用,掌握工序质量特性分布变动的状态。它主要适用于零件尺寸、产品重量 、热处理后机械性能、材料成分含量等服从正态分布的质量特性的控制。

做出 图x 及R图的坐标系,并将横坐标样本号单位对齐,将表6中各样本的、xiRi在图上打点,联结点成平均值、极差波动曲线,图5即为分析用控制图。
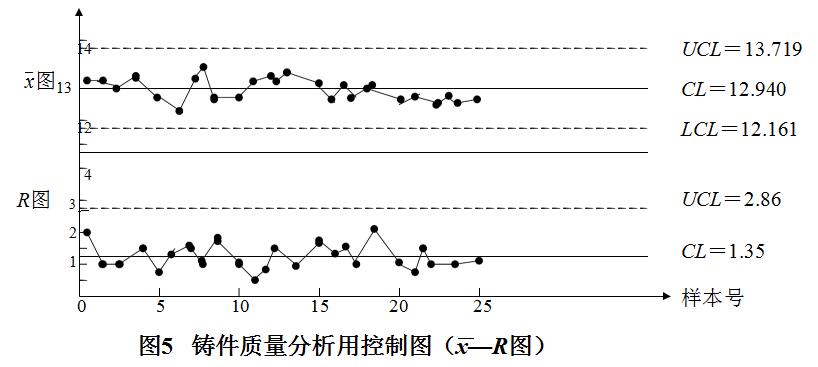
根据本节“控制图的观察与判断”标准,工序处于稳定状态。由表6给出的数据,进而可计算出工序能力指数。


L—S控制图(两极控制图)
原理:它是通过极大值,极小值的变化掌握工序分布变化的状态。其适用场合与 X-R控制图相同。但因只用一张图进行控制,因此具有现场使用简便的优点。

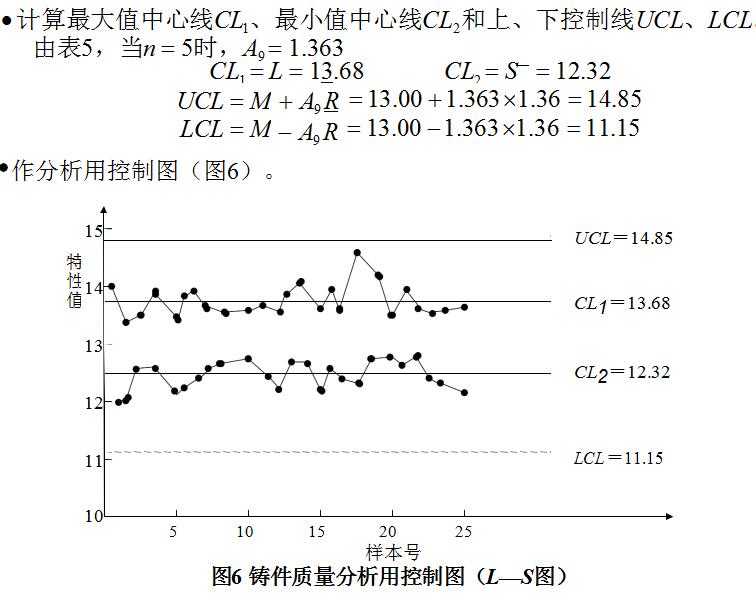
x-Rs控制图(单值—移动极差控制图)
应用范围:它适用于质量特性值不易取得的情况。如抽取的样本是一种混合均匀的液体、或质量特性值的取得要花费较长时间、较高费用(如破坏性检 查)、产品加工周期长等场合。x图可不通过计算直接在图上打点并能及时发现异常, 但不易发现工序分布中心的变化。
例4 某化工厂决定对某化工产品中的甲醇含量采用x-Rs控制 图进行控制。每天取一 个样本,样本容量n=1,共抽取样本26个,测得的预备数据如表7所示。试作x-Rs分析 用控制图。

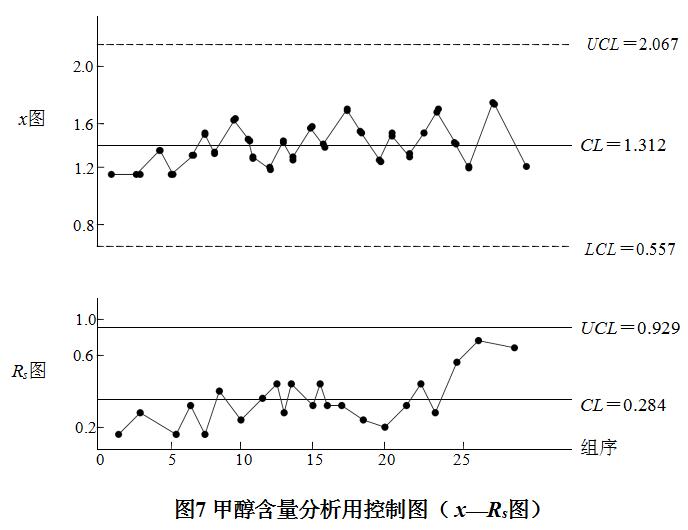
p控制图(不合格品率控制图)
原理:属计件值控制图,它是通过工序不合格品率对工序进行分析与控制的。
例5 某车间采用p控制图对锻件不合格品率p进行控制,统计了近期生产的24批(即 24 个样本)锻件质量情况,各批批量大小(即样本大小ni)及不合格品数pni如表 8所示。试作分析用控制图。


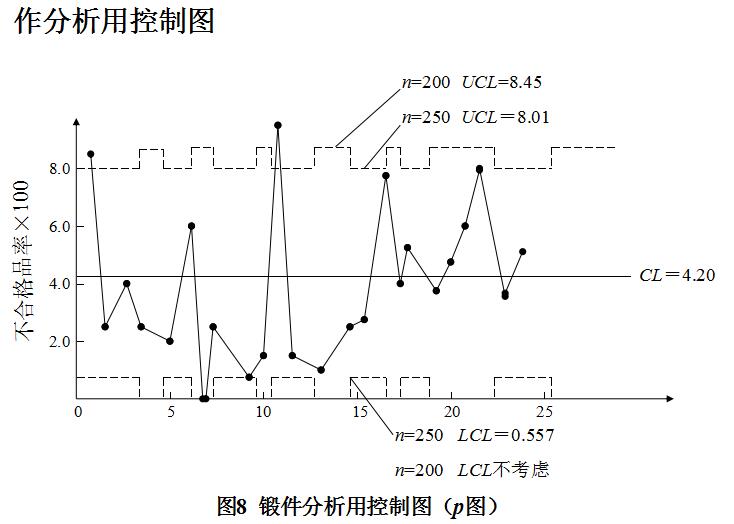
由图可见,由于ni不一致,因此上下控制线是一对对称的折线。为简化计算与作图,应尽 可能使ni一致。当ni不一致但却满足如下条件: