快速学习过程能力指数Cp与Cpk计算原理

关键词：过程能力指数,Cp,Cpk

过程能力也称工序能力，是指过程加工方面满足加工质量的能力，它是衡量过程加工内在一致性的，最稳态下的最小波动。

过程能力概述：

过程能力也称工序能力，是指过程加工方面满足加工质量的能力，它是衡量过程加工内在一致性的，最稳态下的最小波动。当过程处于稳态时，产品的质量特性值有99.73%散布在区间[μ-3σ，μ+3σ]，（其中μ为产品特性值的总体均值，σ为产品特性值总体标准差）也即几乎全部产品特性值都落在6σ的范围内﹔因此，通常用6σ表示过程能力，它的值越小越好。

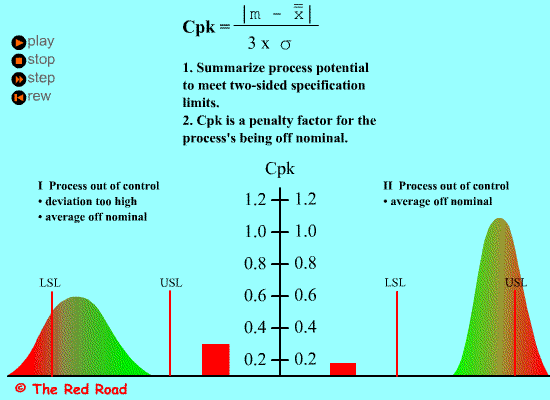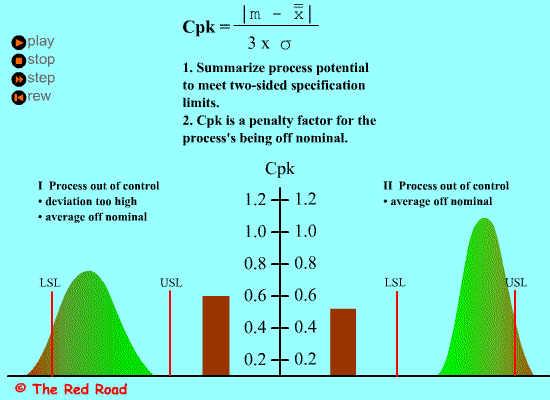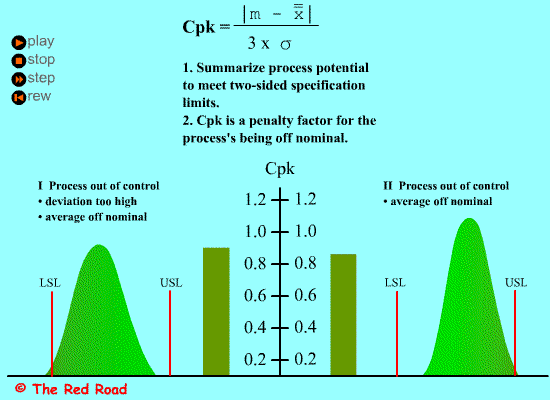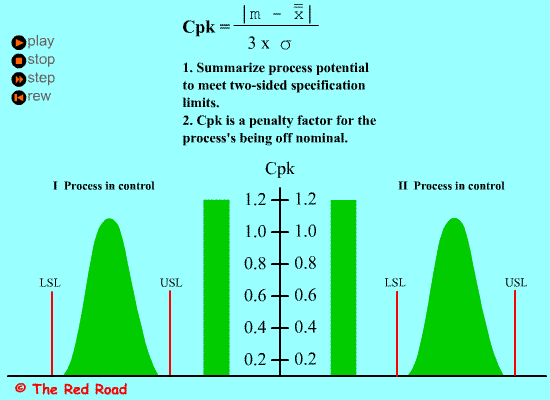
过程能力指数Cp的定义及计算：

过程能力指数Cp是表征过程固有的波动状态，即技朮水平。它是在过程的平均值μ与目标值M重合的情形，如下图所示：

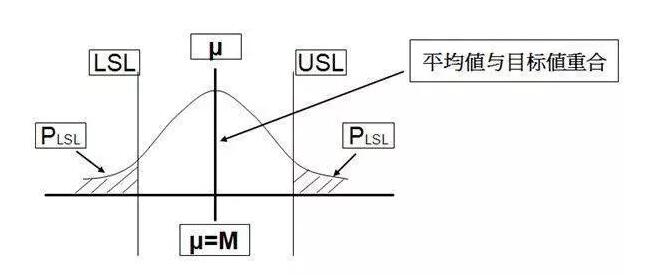
过程处于统计控制状态时，过程能力指数Cp可用下式表示：

Cp = (USL-LSL)/6σ

而规格中心为M=(USL+LSL)/2，因此σ越小，过程能力指数越大，表明加工质量越高，但这时对设备及操作人员的要求也高，加工成本越大，所以对Cp值的选择应该根据技朮与经济的综合分析来决定。一般要求过程能力指数Cp≧1，但根据6Sigma过程能力要求Cp≧2，即在短期内的过程能力指数Cp≧2。

例：

某车床加工轴的规格为50±0.01mm，在某段时间内测得σ =0.0025，求车床加工的过程能力指数。 

Cp = (USL-LSL)/6σ

     =0.02/ (6*0.0025)

     =1.33

过程能力指数Cpk的定义及计算

上面我们讨论了Cp，即过程输出的平均值与目标值重合的情形，事实上目标值与平均值重合情形较为少见；因此，引进一个偏移度K的概述，即过程平均值μ与目标值M的偏离过程，如下图所示：

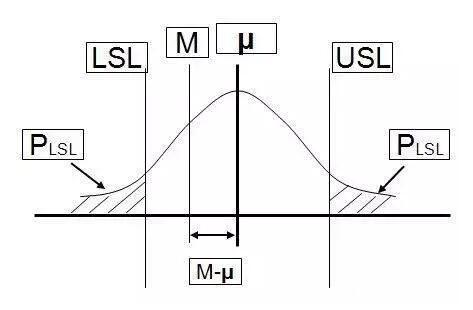
K=|M-μ|/(T/2) = 2|M-μ|/T (其中T=USL-LSL)

Cpk = (1-K)*Cp= (1-2|M-μ|/T)*T/6σ

       =T/6σ-|M-μ|/3σ

从公式可知： 

Cpk=Cp-|M-μ|/3σ，即Cp-Cpk=|M-μ|/3σ，尽量使Cp=Cpk，|M-μ|/3σ是我们的改善机会。

例：

某车床加工轴的规格为50±0.01mm，在某段时间内测得平均值μ=49.995，σ=0.0025，求车床加工的过程能力指数。 

Cpk =T/6σ- |M-μ|/3σ

       =0.02/ (6*0.0025)-|50-49.995|/ (3*0.0025)

       =1.33-0.667

       =0.676

PPK与CPK定义，差异分析及计算

定义：

PP （Performance Index of Process）不考虑过程有无偏移，容差范围除以过程性能。

Cpk （Preliminary process Capability）考虑过程有偏差时，样本数据的过程性能。

*ppk 通常用来与cp及Cpk对比，度量和确认内改进的优先次序。

适用环境

ppk：过程性能指数，表示的是过程在一段时间内的表现

1:输出满足规格要求+预测图形+长期不稳定过程（不要求过程稳定）

2:小批生产（试产）的过程性能评价，要求Ppk>1.67；

3·用于实时过程性能研究和初始过程能力评估.

Cpk：过程能力指数，表示过程本身的能力，一种理想的状态下的指数。

1:过程稳定+足够历史数据/初始数据（More than 100个体数据&25子组

2:大批量生产后的生产能力的评价，要求Cpk>1.33

3:主要用于周期性的过程评价.

注解：

1、有时CPK需要借助PPK的控制界限来作控制

2、PPK表示所有数据之间的变差；CPK剔除组内变差（组内均值），仅考虑子组变差。

3、PPK和CPK的区别就好像是一个人的工作表现和工作能力之间的差别一样。

4、Cpk计算之前，一定要检查过程是否稳定。一般要求有100个数据，25个均值。

取样方式：子样定间隔时间选取（如：每隔1小时连续取4个样本，计算均值。通过xbar-R图来检查过程是否稳定。如果稳定，计算得到的是Cpk。

5、PPK不要求检查过程是否稳定。

取样方式：无需1小时间隔，连续取100个数据。

因PPK未检查过程是否稳定（风险），要求目标PPK>1.67.

因PPK中可能有特殊原因变差不能称之为过程能力指数，而是过程性能指数。

6、过程不稳定，则需查明特殊原因并消除后重新进行评估（过程繁琐）。对于初期数据匮乏案例，在客户同意后可采用PPK。

7、当过程稳定+CPK满足要求时，利用控制图来监视过程。过程实际运行有可能发生特殊原因，一旦发现就要查明后消除它，使过程回到稳定。

8、当过程运行相当长一个时期以后，要定期检查CPK>1.33。通常长期CPK<短期CPK，这是由于计算数据中的标准差数值变大导致的。

CPK的计算

CPK计算前提：变异（或波动），因为有变异的存在，才区分能力大小。

变异种类：

1.普通原因变异：平时一直客观存在，对过程有一定的影响但不明显。

2.特殊原因变异：偶然出现，对过程影响很大。

举例说明 : 空调房设温度25度，由于室内外温差，时刻会有能量交换，所以室内温度实际可能在一定范围（微小）内变化（24.99，24.98，25.00，25.0..时即是普通因素的影响，而有人推门进来，室内温度瞬间产生较大变化，此时即是同时受到普通因素和特殊因素影响。

过程表现：

若只受普通因素影响则控制图上过程受控，

如有特殊原因的影响则控制图上会有异常点出现。

CP/CPK使用前提：过程稳定+正态分布+数据25组以上，只考虑过程受普通因素的影响。

*建议最少不低于20组（数据组越少采信结果的风险越大）

计算公式：

注解：

1，PP，PPK的计算公式与CP，CPK计算公式相同。

2、区别：变差（标准差）σ的计算方式不同。

PPK时，。为标准差公式计算得来；cpk时，σ-R/d2度差=子组极差均值/变差常数]PPK的变差包括普通因素和特殊因素产生的两种变差，对相同工程而言大于CPK变差。因此理论上CPK= PPK，但实际使用minitab时会出现PPK略大于CPK，因为CPK的变差是估算的，存在误差。（不影响对最终过程能力大小的评价）

3、过程只受到普通因素变差影响是理想状态，过程总会受到各种特殊因素的影响，因此可分别称CP/CPK（短期过程能力/潜在过程能力），PP/PPK长期过程能力/性能指数

4、因为PP/PPK不需要过程稳定（在计算公式中已经考虑了普通和特殊两种因素的影响），所以PPAP要求试产过程不稳定时使用PPK衡量过程能力。

只有PPK＞1.67才能进入量产阶段，所以PPK又称为 期能力指数。

5、进入量产后应同时监控CP/CPK/PPK三个指数的区别进而断过程是否有问题、管理问题还是技术问题。

举例说明：

a. 当CP> 1.33，表明过程变差比较小（USL-LSL是规格确定值），此时同时检测CPK，若CP和CPK相差很大，则说明过程便宜较大，需要做居中处理。

再比较CPK和PPK，若两者相差不大则过程受特殊因素的影响小，反之影响很大。

b. 特殊因素的影响往往比较容易找到，但如果CP本身就很小则说明过程受普通因素的变差影响大，若想提升过程能力则需要更多的投入和更高的决策才能解决问题。

因此即使cpk值很高（比如大于2），如果其与CP/CPK相差较大则需改进过程。

c. 若CPK比PPK则：1过程没有受控2控制图上有异常点3.计算人员错用了结论。

PPK和CPK的区别点：

1、δ的计算公式不同，PPK采用标准差，CPK用经验公式（偏差很小）

2、取样方法不同：PPK要短时间内连续生产的，CPK一般是每天取一组数据（一般5个）。