特性分析到CPK计算到，完整的spc统计过程控制案例

关键词：CPK，SPC，PFMEA

1 小明接到的任务

小明，就是那个小学数学很差，总是一边往池塘里注水一边还放水的沙雕，大学毕业后是一名苦逼机械工程师。一天，他接到了这样一个任务：

顾客要求小明生产一个衬套，衬套内圈要和对手件过盈配合，并且满足1kN推出力要求，顾客提供对手件尺寸∅30p6（+0.035，+0.022）。

装配件示意图如下，红色环形件为衬套，与对手件轴销成过盈配合：

2 编制DFMEA

对任务有了一定了解之后，按照汽车行业通用DFMEA模板，小明针对衬套内径编制了DFMEA：

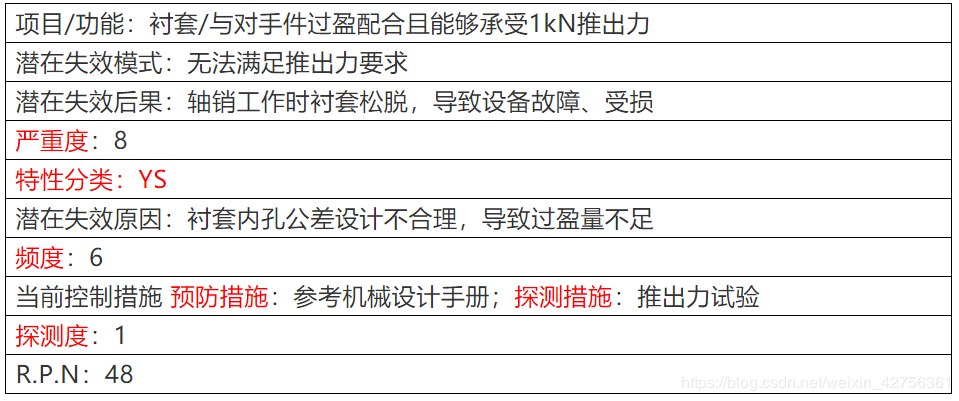
在编制DFMEA时，小明考虑到一旦发生失效，衬套松脱可能导致设备损坏，所以严重度打分8分。又由于缺乏设计经验，不确定多大的过盈量才能满足推出力要求，所以失效频度打分6分。由此，衬套内孔被定义为YS项。内孔直径的设计参考机械设计手册，最终通过推出力试验验证设计是否可行。

3 编制PFMEA

通过DV试验，小明给出了衬套内孔的设计∅30H7（∅30 +0.021/0）。下一步进入生产阶段，小明对内孔加工给出的工艺为粗车+精车，精车完成最终加工。由此针对这一工序编制PFMEA：

在编制PFMEA时，过程失效的严重度等级继承设计失效的严重度等级，仍为8；由于车削时材料已经过热处理，硬度较大，车刀磨损剧烈，尺寸不易控制，因此失效频度打分5。衬套内孔直径在PFMEA中被定义为SC项。除定期更换车刀，对SC项还应当采取SPC措施。

4 确定测量方法

为了尽可能细致的获得内径尺寸的分布，小明选择使用数显孔径千分尺对内径进行测量，精度0.001，满足测量仪器精度应当小于被测对象公差1/10~1/5的要求。通过反复测量标准试样，证明所选用的量具是合格的（一个简易的MSA）。

5 制定SPC计划

在小批量试产前，小明制定了初步的SPC计划：衬套内孔直径为连续型变量，采取均值-极差图，抽样频率为生产50件抽取一次样本，样本容量为5。

6 生产预期

生产前小明通过检查生产设备，操作人员资质，及对若干试制件进行全尺寸检验，排除了可能存在的特殊原因。批产中最大的风险应当是车刀磨损这一系统原因，也是SPC过程控制中最需要监控的项目之一。

7 数据采集与处理

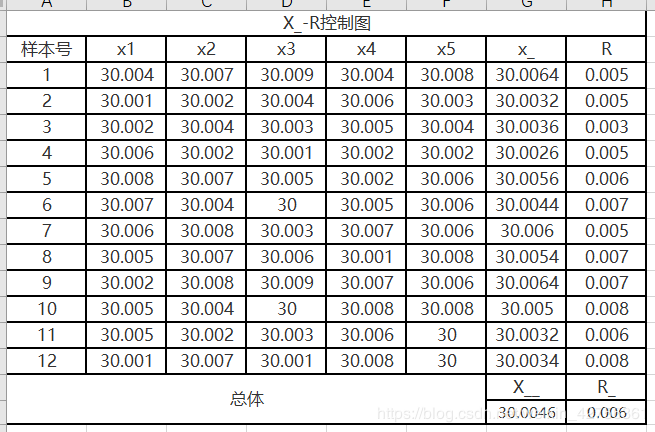
在制造部的帮助下，在小批量生产中小明采集到了如下数据，并计算每组样本的均值X_和极差R以及总体的均值X__和极差R_。

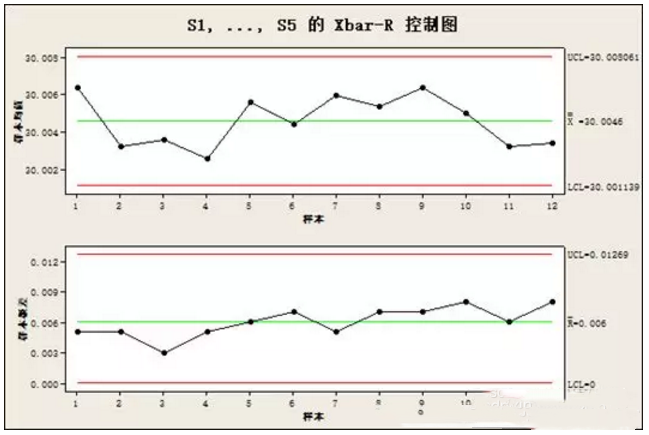
按照SPC教程，小明绘制了均值-极差控制图，如下：

8 过程是否稳定的判据

SPC给出了一个过程稳定的几个判定依据：

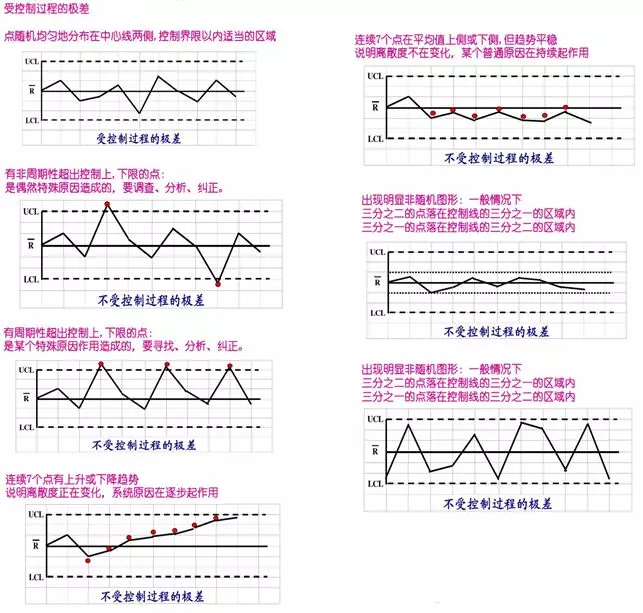
通过一一比对不稳定过程存在的特性，小明得出结论：在这一批次生产中过程是稳定的。

9 计算过程能力CPK

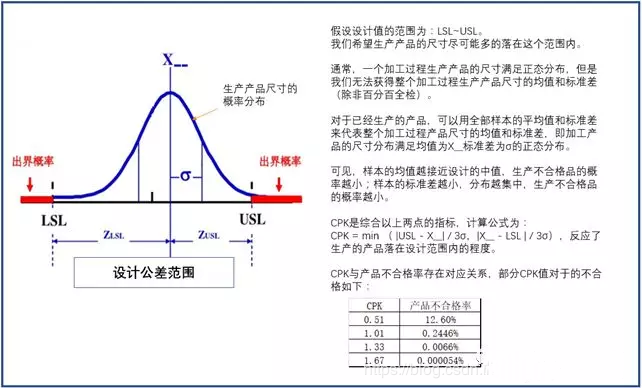
下面的三个案例展示了样本尺寸不同的分布如何影响CPK的值，假设目标范围9~11，C均值为10，标准差0.3，计算CPK为0.92；C2均值为10，标准差1，数据分布分散，计算CPK为0.36；C3均值为9.7，标准差0.3，数据偏离目标中心，计算CPK为0.82。

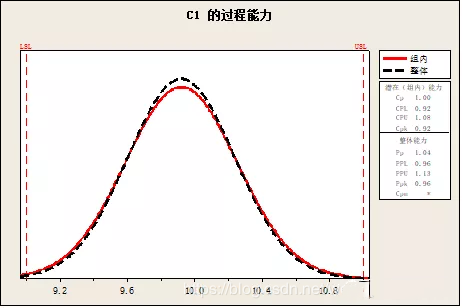
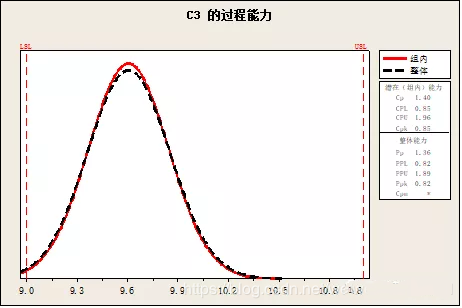
在小明的例子里，设计范围：∅30H7（∅30+0.021/0）

所有样本均值X__=30.0046

按Rbar计算标准差标准差σ=0.00258

CPK=min(|30.021-X__|/3σ，|X__-30|/3σ)=0.59

使用Minitab计算的CPK，PPK如下：

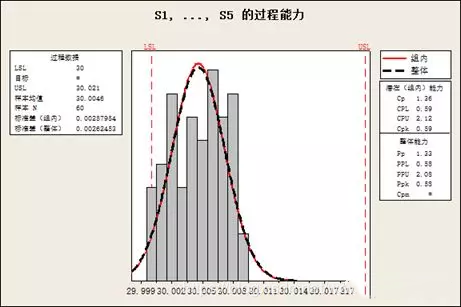
可见，尽管工艺过程是稳定的，但是CPK值很低。当CPK=0.51时，所生产产品的不合格率约为12.6%，这个不合格率显然是不能接受的。这种情况可以理解成：过程将稳定的提供12.6%的不合格的产品。小明还需要通过优化工艺提高工艺的过程能力。

10 改进的方法

从过程能力图来看，工艺的均值偏离目标中值过大，这是导致不合格过高的主要原因。K=|工艺均值 – 目标中值|/（USL - LSL）=| 30.0046-30.0105 |/（30.021 - 30）= 28.1%，K称之为偏离度，是反应测量中值偏离目标中值程度的常数。首先应当通过调机使K值小于12.5%。

工艺的Cp值=1.36>1.3，当K满足K<12.5%时，无需做额外调整。因此，小明只需要通过调机使测量中值与目标中值接近即可，如果仍不能满足要求，需要采取其他手段进一步提高过程能力。