从小概率事件的角度分析SPC控制图

关键词：SPC,控制图, SPC控制图

如何分析SPC控制图，利用SPC控制图揭示过程质量的原理是什么？这里有两种解释。第一种解释是小概率事件，第二种解释是偶然波动与异常波动。本文主要介绍从小概率事件的角度分析SPC控制图。

以生产螺丝为例。为了控制加工螺丝的质量，设每隔一个小时随机抽取一个车好的螺丝，测量其直径，将测量结果描点在SPC控制图中，并用直线段将点子连接，以便观察点子的变化趋势。由下图可以看出，前3个点子都在控制限内，但第四个点子却超出了UCL，为了醒目，把它用小圆圈圈起来，表示第四个螺丝的直接过分粗了，应引起注意。现在对这第四个点子应做什么判断呢？摆在面前的是两种可能：
 

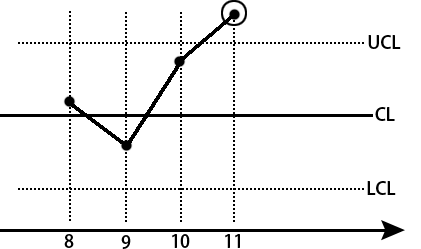
从小概率事件的角度分析SPC控制图

1、    若过程正常，即分布不变，则点子超出UCL的 概率只有1.35‰。

2、    若过程异常，譬如设异常原因为车刀磨损，则随着车刀的磨损，加工的螺丝将逐渐变粗，μ逐渐增大，于是分布曲线上移，点子超出UCL的概率将大为增加，可能为1.35‰的几十、几百倍。

现在第四个点子已经超出UCL，问题是：在上述两种情况中，应该判断是哪种情况造成的。由于情况2发生的可能性要比情况1大几十、几百倍，故按照常理，认为上述异常是由情况2造成的。于是得出结论：点出界就判异，并把它作为一条判异准则来使用。用数学语言来说，这就是小概率事件原理：小概率事件实际上不发生，若发生则判断异常。SPC控制图就是统计假设检验的图上作业法。

以上就从小概率事件的角度分析了SPC控制图。首先假设过程正常或过程异常，然后比较两者发生的概率，通常异常发生的概率（小概率事件）要远远大于正常发生的概率，因此点子出界即判定过程异常，接下来就是采取纠正措施，使生产过程恢复正常。