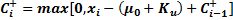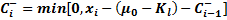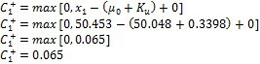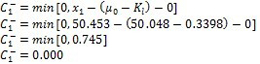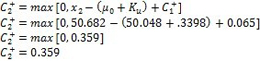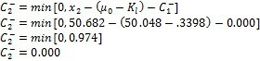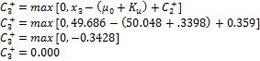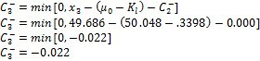2017-08-17
表格式累积和(CUSUM)图
|
关键词:表格式累积和图,控制图 导语:和控制图一样,表格式累积和图以时间为顺序记录数据的。表格式累积和图的主要优势是更加灵敏地侦测均值的微小偏移,相比单值移动极差图,这一点尤其明显。 十九世纪二十年代,在西部电子公司供职的沃特•休哈特博士创建了第一张控制图。距今,控制图已经使用将近 100 年。1931年,休哈特博士出版了具有里程碑意义的《产品制造质量的经济控制》一书,奠定了现代统计质量控制方法的基础。 今天,很多质量控制方法都是对休哈特的技术的改进。所有这些改进都是为了更好地支持现代生产方法和挑战。其中一种图是表格式累积和图,或简称为累积和(CUSUM)图。 |
| 什么是累积和图? |
| 和控制图一样,累积和图以时间为顺序记录数据的。图表在过程发生显著变化时警示用户。累积和图不使用原始数据、均值、极差或标准差记录数据,取而代之的是有代表性的近似数据,子组和子组与指定目标或产品均值的偏差的累积和的数据。表格式累积和图的主要优势是更加灵敏地侦测均值的微小偏移,相比单值移动极差图,这一点尤其明显。 |
| 为什么使用累积和图? |
|
基本上,使用积累和图的原因可以归结为敏感性。通常认为均值极差图和均值标准差图是过程控制的有力工具。这种效力基于:随着子组样本数 n 的增加,均值的分布趋近于正态分布。子组样本数越大,均值图对均值显著偏移越敏感。提高控制图敏感性和提高子组样本数一样简单。但是,不是所有人都可以使用提高子组样本量这样的奢侈方式。比如,生产车间生产的产品是短制程生产,或者产品的质量检测是破坏性的实验。在这种情况下,可以获得的数据很少,或者出于成本的考虑,数据难以采集,因此无法提高样本容量。 如果子组大小不能提高,那么单值、移动极差(IX-MR)图就会是比较好替代均值极差图的选择。然而,因为在单值图上,描点为单值(不是平均值),单值图对于总体均值的微小偏移敏感性很差,特别是与均值图相比较。 累积和图普遍使用的另一个原因是可以减低风险。比如,有的公司生产的产品如果偏离目标值太远,将导致灾难性的后果。这些组织将不能等到数据超出+/-3σ控制限才生成警报。因此,他们需要对微小的过程变化更加敏感。 上面的理由表明累积和图的有效性。在均值发生很小(1 - 1.5σ)的变化时,必须识别出来。在控制过程的数据很少时,累积和图是出色的解决方案。目前,累积和图已被广泛应用于航空、冶金、化工和连续流程性行业。 |
| 如何生成累积和图? | ||||||||||||||||||||||||||
和传统的控制图比,表格式累积和图是独特的,在生成累积和图的过程中,必须使用特定的参数和统计信息。
|
||||||||||||||||||||||||||
| 表格式累积和图范例 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
钢铁公司为建筑行业生产大量的工字钢。工字钢形状巨大,生产成本高昂,而且不是经常生产。作为关键质量特性,“A-尺寸”难于测量,但又必须严格控制。 如果A-尺寸平均值有超过目标值向上偏移为 1σ,产品的强度会损坏,且产品只能报废。如此一来将造成巨大的经济损失。为了防止出现这种情况,公司要求在A-尺寸平均值偏离目标值至少一个σ时提示操作员。 在历史上,A-尺寸的平均值接近50.00,历史标准偏差为约为 0.70。下面是最近采集的 28 个A-尺寸的值,见下表。在21-28子组中带有星号,表示均值从 50.00 变到50.75 ,大约增加了一个σ。
在图3中看到A-尺寸数据的传统的 IX-MR 控制图。蓝色的垂直标记表示A-尺寸均值开始了持续的 1σ的增长。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
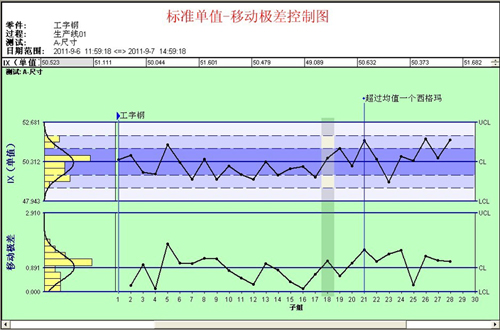 图3 A-尺寸数据的IX-MR 控制图 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
尽管在单值移动极差控制图上,最后八个A-尺寸的尺寸值确实有1σ的增长,但没有数据落在控制限之外。这种偏差在单值图上是很难察觉的,因为当子组样本量很小的时候,单值图在感知均值的微小改变上存在天生的缺陷。 为了验证表格式累积和图的优越性,使用表格2中同样的数据,完成下面的例子。 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 创建表格式累积和图 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
创建累积和图需要下面几个步骤:
第一,根据范例工字钢的描点值计算的累积和图上的描点值,显示如表4。
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| 绘图点 | ||||||||||
下面是完成工字钢例子的累积和图所必须的假设和计算:
使用下面的公式计算上下绘图点作为开始: |
||||||||||
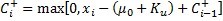 |
||||||||||
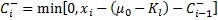 |
||||||||||
每个绘图点取下面结果中较大的值:
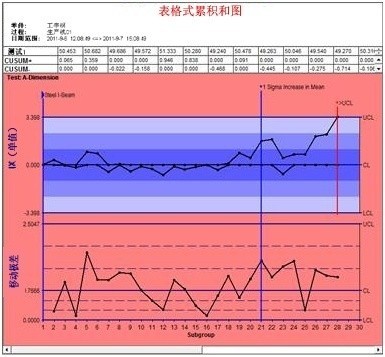
上下累积和图值计算后,将它们绘制在同一图表上(见图6)。 |
||||||||||
 |
||||||||||
|
表6在表格式累积和图上的工字钢A-尺寸数据 |
||||||||||
| 理解表格式累积和图 |
|
在上面的图中,需要注意到那与众不同的双线条,这个累积和图看起来和休哈特的控制图非常相似。这也是该图吸引人的地方。两个不同的绘图点让钢铁制造商可以同时看到累积和上、下偏离目标的情况。而这样的绘图点仅仅在上面的图中计算,累积和图的计算对下面的移动极差没有影响。如果在均值上没有明显的偏移,累积和图点将围绕中心线 0 波动。在前 20 个绘图点的情况就是这样。 回顾前面的数据,前二十个子组的数据均值为 50.048,估计标准差 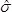 为 0.6796。从21个 到28 个子组,均值变为 50.75。A-尺寸均值增长了 1σ多一点。 为 0.6796。从21个 到28 个子组,均值变为 50.75。A-尺寸均值增长了 1σ多一点。钢铁公司特别关心均值相对于目标值的增长。不像图3的单值移动极差图那样,累积和图触发警报,表示均值上升大于1σ。总体上,和前面的数据相比,第20个子组后的数据落点远远高于中心线。这也进一步证明均值出现了连续的上升。 此外,最后4个绘图点稳定地上升,直到最后一个绘图点超过上控制限(H 值 = 5 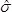 = 5(.6796) = 3.398)。不像在单值移动极差控制图上的独立点,每个累积和图值受到前面的数值的影响。 单值移动极差不是这样的。这样可以使表格式累积和图对均值微小的变化更加敏感。 = 5(.6796) = 3.398)。不像在单值移动极差控制图上的独立点,每个累积和图值受到前面的数值的影响。 单值移动极差不是这样的。这样可以使表格式累积和图对均值微小的变化更加敏感。 |



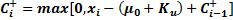
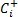 数据点是用来排除在表格累积和图上超过上限的数据点。上限用来识别超过过程目标值
数据点是用来排除在表格累积和图上超过上限的数据点。上限用来识别超过过程目标值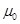 的变化。
的变化。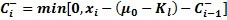
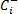 数据点是用来排除在表格累积和图上超过上限的数据点。上限用来识别超过过程目标值
数据点是用来排除在表格累积和图上超过上限的数据点。上限用来识别超过过程目标值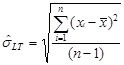
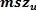
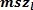
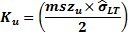
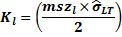
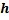
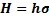
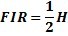
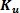 = 上参考值 =
= 上参考值 = 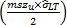 =
= 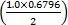 = 0.3398
= 0.3398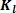 = 上参考值 =
= 上参考值 = 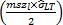 = = 0.3398
= = 0.3398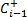 )。
)。