2017-08-17
Kruskal-Wallis (KW) 测试
|
Kruskal-Wallis (KW) 测试主要用来对比三组或更多独立数据组非参数型测试。它用来测试零假设是否成立,原假设的内容是所有的总体具有相同的分布函数,备择假设是至少有两个样本分布不同。InfinityQS SPC 软件使用 KW 来测试多组数据波动性的差异。就是说,KW测试仅对跟踪波动性(移动极差,均值和西格玛图)的图形上的数据的进行处理。它与参数独立数据组方差分析(单因子方差分析)不同,此参数独立测试不进行关于数据分布的假设。这和其它非参数性测试一样,它不使用原始数据进行统计计算,而是使用数据的排序来进行统计计算。由于此测试不进行分布假设,因此它并不像方差分析那样有效。 Kruskal-Wallis 测试的测试统计量为 H。 此值会与表(X2 表)中的临界值进行比较。 如果 H 在某个显著性水平上超过了临界值(InfinityQS使用 0.01) ,说明有充分的证据证明至少有一组数据的波动水平与其它组有明显的差异。 |
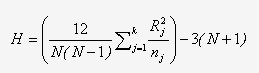 |
参数:
|
| KW 计算举例 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
假设有如下一组数值:
对所有数值做排列:
将排列位值累加:
代入方程式: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
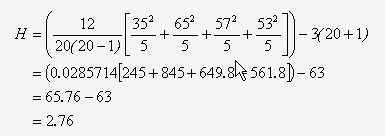 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
将 2.76 在卡方表中可以查到 d.f. = k-1 = 4-1 = 3 在这里, p值 > 0.01,因此,InfinityQS 将显示为“接受”。表示不同机器之间的数据波动没有明显差异。 InfinityQS 将显示实际 p 值。 |


